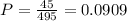Question

Suppose that after I wrote this problem, Richard Rusczyk thought he could be more clever than I could, so he wrote his own problem. Suppose that both of our problems are in the set of 12 problems you are currently working on. If you sat down at your computer this morning and randomly loaded 4 of the 12 problems, what is the probability that both this problem and Richard Rusczyk's problem were among the four you loaded?

Answer 1

P = 0.0909

Explanation:

To know the number of ways or combinations in which we can select x elements from a group of n elements, we can use the following equation:

`nCx=(n!)/(x!(n-x)!)`

So, if you sat down at your computer and randomly loaded 4 of the 12 problems, there are 495 different possibilities and it is calculated as:

`12C4=(12!)/(4!(12-4)!)=495`

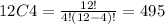
Then, from 495 different possibilities, there are 45 possibilities that both this problem and Richard Rusczyk's problem were among the four you loaded. This 45 possibilities are calculated as:

`(1C1)*(1C1)*(10C2)=((1!)/(1!(1-1)!))*((1!)/(1!(1-1)!))*((10!)/(2!(10-2)!))=45`

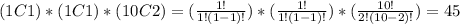
Because you need to select: this problem and there is only one, the problem that Richard Rusczyk wrote and there is only one, and 2 problems from the other 10.

Finally, the probability that both this problem and Richard Rusczyk's problem were among the four you loaded is equal to:

`P=(45)/(495)=0.0909`