Question

A marketing consultant was hired to visit a random sample of five sporting goods stores across the state of California. Each store was part of a large franchise of sporting goods stores. The consultant taught the managers of each store better ways to advertise and display their goods.

The net sales for 1 month before and 1 month after the consultant's visit were recorded as follows for each store (in thousands of dollars):

Before visit: 57.1 94.6 49.2 77.4 43.2
After visit: 63.5 101.8 57.8 81.2 41.9

Do the data indicate that the average net sales improved? (Use a= 0.05)

Answer 1

`t=(\bar d -0)/((s_d)/(√(n)))=(4.94 -0)/((3.901)/(√(5)))=2.832`

`df=n-1=5-1=4`

`p_v =P(t_((4))>2.832) =0.0236`

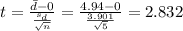
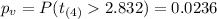
We see that the p value is lower than the significance level of 0.05 so then we have enough evidence to reject the null hypothesis and we can conclude that the average net sales improved

Explanation:

Let put some notation

x=test value before , y = test value after

x: 57.1 94.6 49.2 77.4 43.2

y: 63.5 101.8 57.8 81.2 41.9

The system of hypothesis for this case are:

Null hypothesis:
`\mu_y- \mu_x \leq 0`

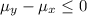
Alternative hypothesis:
`\mu_y -\mu_x >0`

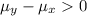
The first step is calculate the difference
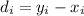`d_i=y_i-x_i` and we obtain this:

d: 6.4, 7.2, 8.6, 3.8, -1.3

The second step is calculate the mean difference

`\bar d= (\sum_(i=1)^n d_i)/(n)=4.94`

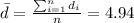
The third step would be calculate the standard deviation for the differences, and we got:

`s_d =(\sum_(i=1)^n (d_i -\bar d)^2)/(n-1) =3.901`

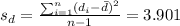
The next step is calculate the statistic given by :

`t=(\bar d -0)/((s_d)/(√(n)))=(4.94 -0)/((3.901)/(√(5)))=2.832`

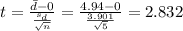
The next step is calculate the degrees of freedom given by:

`df=n-1=5-1=4`

Now we can calculate the p value, since we have a right tailed test the p value is given by:

`p_v =P(t_((4))>2.832) =0.0236`

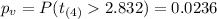
We see that the p value is lower than the significance level of 0.05 so then we have enough evidence to reject the null hypothesis and we can conclude that the average net sales improved