Answer:
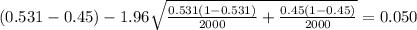
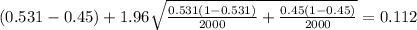
And the best option for this case would be:
A. 0.050 to 0.112.
Explanation:
Data given
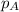 represent the real population proportion of who support the cnadite for the northern half state
represent the real population proportion of who support the cnadite for the northern half state
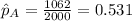 represent the estimated proportion of who support the candidate for the northern half state
represent the estimated proportion of who support the candidate for the northern half state
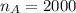 is the sample size required the northern half state
is the sample size required the northern half state
 represent the real population proportion of who support the candidate for the southern half state
represent the real population proportion of who support the candidate for the southern half state
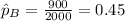 represent the estimated proportion of people who support the candidate for the southern half state
represent the estimated proportion of people who support the candidate for the southern half state
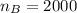 is the sample size for the northern half state
is the sample size for the northern half state
 represent the critical value
represent the critical value
The confidence interval for the difference of two proportions would be given by this formula
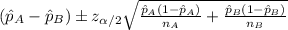
For the 95% confidence interval the value of
 and
and
 , with that value we can find the quantile in the normal standard distribution and we got.
, with that value we can find the quantile in the normal standard distribution and we got.
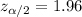
Replacing into the formula we got:
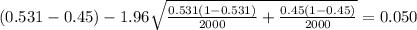
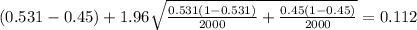
And the best option for this case would be:
A. 0.050 to 0.112.