Question

A block of plastic in the shape of a rectangular solid that has height 8.00 cm and area A for its top and bottom surfaces is floating in water. You place coins on the top surface of the block (at the center, so the top surface of the block remains horizontal). By measuring the height of the block above the surface of the water, you can determine the height hh below the surface. You measure hh for various values of the total mass mm of the coins that you have placed on the block. You plot h versus m and find that your data lie close to a straight line that has slope 0.0890 m/kg and y-intercept 0.0312 mm.

What is the mass of the block?

Answer 1

m_{p} = 0.3506 kg

Step-by-step explanation:

For this exercise we use Newton's equilibrium equation

B - Wc-Wp = 0

where B is the thrust of the water, Wc is the weight of the coins and Wp is the weight of the plastic block

B = Wc + Wp

the state push for the Archimeas equation

B = ρ_water g V

the volume of the water is the area of ​​the block times the submerged height h, which is

h´ = 8 - h

where h is the height out of the water

ρ_water g A h´ =
`m_(c)` g +
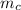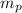`m_(p)` g

ρ_water A h´ = m_{c} + m_{p}

write this equation to make the graph

h´= 1 /ρ_water A (m_{c} +m_{p})

h´ = 1 /ρ_waterA (m_{c} + m_{p})

if we graph this expression, we get an equation of the line

y = m x + b

where

y = h´

m = 1 /ρ_water A

b = mp /ρ_water A

whereby

m_{p} = b ρ_water A

ρ_water = 1000 kg / m³

b = 0.0312 m

m = 0.0890 m / kg

we substitute the slope equation

b = m_{p} / m

calculate

m_{p}= 0.0312 / 0.0890

m_{p} = 0.3506 kg