Question

Prove, using the second derivative, that the general quadratic y= ax^2+bx+c, is:

a) always convex when a>0
b) always concave when a <0

Answer 1

There are three things you have to know:

• A function is convex when its second derivative
  `f''(x)>0`
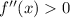
• A function is concave when it second derivative
  `f''(x)<0`
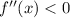
• The derivative of a power,
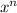  `x^n`, is
  `nx^(n-1)`

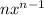
So, the first derivative is

`y'=2ax+b`

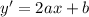
and the second derivative is

`y''=2a`

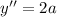
This implies that the second derivative of a parabola is constant, and of course that 2 doesn't change the sign of
`a`.