Question

Sin(x)^2 = cos(x/2)^2

Answer 1

First of all, you can use

`\sin^2(x)+\cos^2(x)=1 \iff \sin^2(x)=1-\cos^2(x)`

and the equation becomes

`1-\cos^2(x)=\cos^2\left((x)/(2)\right)`

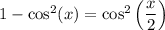
Now, from the known identity

`\cos^2(x)=(1+\cos(2x))/(2)`

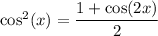
we can half all the angles and we get

`\cos^2\left((x)/(2)\right)=(1+\cos(x))/(2)`

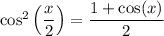
So, the equation has become

`1-\cos^2(x)=(1+\cos(x))/(2) \iff 2-2\cos^2(x)=1+\cos(x)`

So, everything comes down to solve

`2\cos^2(x)+\cos(x)-1=0`

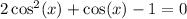
The associated equation

`2t^2+t-1=0`

has roots

`t=-1,\quad t=(1)/(2)`

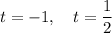
So, we want one of the following

`\cos(x)=-1,\quad \cos(x)=(1)/(2)`

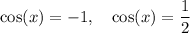
Solve for the associated angles and you're done