Answer:
The distance between ring and coin is 13 units apart.
Explanation:
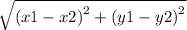
Using this formula, you are able to find the distance between the ring and the old coin :
Let (x1,y1) be (10,19),
Let (x2,y2) be (5,7),
D = √(10-5)²+(19-7)²
= √5²+12²
= √25+144
= √169
= 13 units