Question

The equilibrium constant for the reaction

COCl2 (g) CO (g) + Cl2 (g) is Kc = 4.63 ´ 10–3 at 527 °C
If 10 g of COCl2(g) is placed in a 1 L container, determine how much Cl2 is present at equilibrium.

Answer 1

Answer: The concentrations of
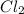`Cl_2` at equilibrium is 0.023 M

Step-by-step explanation:

Moles of
`Cl_2` =
`\frac{\text {given mass}}{\text {Molar mass}}=(10g)/(71g/mol)=0.14mol`

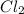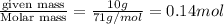
Volume of solution = 1 L

Initial concentration of
`Cl_2` =
`(0.14mol)/(1L)=0.14M`

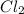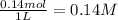
The given balanced equilibrium reaction is,

`COCl_2(g)\rightleftharpoons CO(g)+Cl_2(g)`

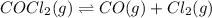
Initial conc. 0.14 M 0 M 0M

At eqm. conc. (0.14-x) M (x) M (x) M

The expression for equilibrium constant for this reaction will be,

`K_c=([CO]* [Cl_2])/([COCl_2])`

Now put all the given values in this expression, we get :

`4.63* 10^(-3)=(x)^2)/((0.14-x))`

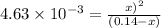
By solving the term 'x', we get :

x = 0.023 M

Thus, the concentrations of
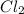`Cl_2` at equilibrium is 0.023 M