Question

In circle A shown, secant DE and tangent DG are drawn. It ir know that m BAC = 63 and mBE = 96.

Answer 1

Givens

`m \angle BAC=63\°`

`m(BE)=96\°`

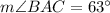
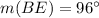
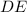`DE` is secant.

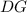`DG` is tangent.

(A)

Remember that the arc subtended by a central angle is equal to it. That means

`m(BC)=m\angle BAC = 63\°`

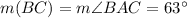
(B)

Now, by sum of arcs, we know

`m(EBC)=m(EB)+m(BC)=96\° +63\°=159\°`

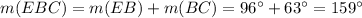
(C)

By definition, the total arc of a circle is 360°, so

`m(EFC)=360\°-m(EBC)=360\° - 159\°=201\°`

(D)

We know that the external angle formed by a secant and a tanget is one half of the difference between the intercepted arcs, so

`\angle D=(1)/(2)(m(EFC)-m(BC))=(1)/(2) (201\° - 63\°)=(1)/(2) (138\°)=69\°`

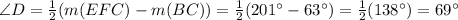
So, the angle D is 69°.