Question

Question 1

4 pts
Which set of line segments could create a right triangle? (4 points)
O 15,30,35
O 15,36,39
O 15, 20, 29
O 5,15,30

Answer 1

(B)15,36,39

Explanation:

To determine which of the line segments could create a Right Triangle, we check if it satisfies the Pythagoras Theorem, taking the longest part to be the Hypotenuse in all cases.

By Pythagoras Theorem:
`Hypotenuse^2=Opposite^2+Adjacent^2`

In 15,30,35

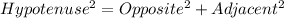
`35^2\\eq 15^2+30^2\\1225\\eq 1125`

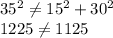
In 15,36,39

`39^2=36^2+15^2\\1521=1521`

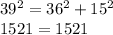
In 15, 20, 29

`29^2\\eq 15^2+20^2\\841\\eq 625`

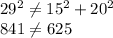
In 5,15,30

`30^2\\eq 15^2+5^2\\900\\eq 250`

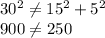
We can see that only 15,36,39 satisfies the required condition and thus it could be used to create a right triangle.