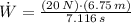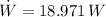Answer:
a)
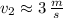 , b)
, b)
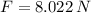 , c)
, c)
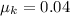 , d)
, d)
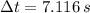 , e)
, e)
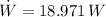
Explanation:
a) La velocidad final se obtiene por medio del Principio de Conservación de la Energía y el Teorema del Trabajo y la Energía (Final speed is determined by means of the Principle of Energy Conservation and the Work-Energy Theorem):
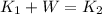
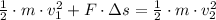
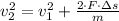
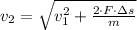
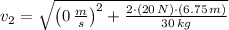
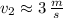
b) La fuerza resultante es determinada por el Teorema del Trabajo y la Energía (Resultant force is obtained by the Work-Energy Theorem):
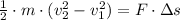
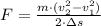
![F = ((30\,kg)\cdot \left[(1.9\,(m)/(s))^(2)-(0\,(m)/(s))^(2)\right])/(2\cdot (6.75\,m))](https://img.qammunity.org/2021/formulas/mathematics/college/fnkhixev7hdug3urvcmf7i7mndriplvdad.png)
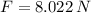
c) Primero, se calcula la fuerza asociada a la fricción (First, the force associated with friction has to be calculated):
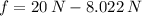
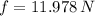
El coeficiente cinético de fricción es (The kinetic coefficient of friction is):
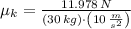
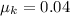
d) La acceleración neta del carrito es (The net acceleration of the car is):
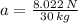
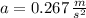
El tiempo requerido es (The required time is):
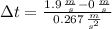
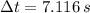
e) La potencia aplicada descontando la fricción es (The applied power neglecting friction is):