Question

Takumi started studying how the number of branches on his tree changes over time.

The relationship between the elapsed time, t, in years, since Takumi started studying his tree, and the total
number of its branches, N(t), is modeled by the following function:
N(t) = 63. 2
Complete the following sentence about the yearly rate of change in the number of branches.
Every year, the number of branches
grows/shrinks
by a factor of

Answer 1

Grows by a factor of 2

Explanation:

Khan Academy

Answer 2

Grows, Factor of 2

Explanation:

The relationship between the elapsed time, t, in years, since Takumi started studying his tree, and the total number of its branches, N(t), is modeled by the function:

`N(t) = 63. 2^t`

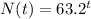
For illustration, let us take the growth for the first three years after he started studying the number of branches.

`When \:t=1, N(1) = 63. 2^1=126\\When \:t=2, N(2) = 63. 2^2=252\\When \:t=3, N(3) = 63. 2^3=504\\504/ 252=252/ 126=2`

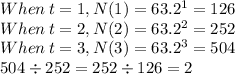
We notice that for each subsequent year, the number of branches doubles.

Therefore:

Every year, the number of branches grows by a factor of 2.