Answer:
A, D and F.
Explanation:
If f(x) is a function and another function is defined as
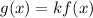
If |k|>1, then it is clear vertical stretch.
If 0<|k|<1, then it is clear vertical compression.
In function
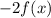 ,
,
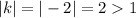 vertical stretch.
vertical stretch.
In function
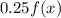 ,
,
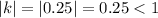 vertical compression.
vertical compression.
In function
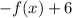 ,
,
 neither stretch nor compression.
neither stretch nor compression.
In function
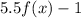 ,
,
 vertical stretch.
vertical stretch.
In function
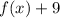 ,
,
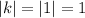 neither stretch nor compression.
neither stretch nor compression.
In function
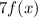 ,
,
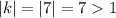 vertical stretch.
vertical stretch.
Hence, the correct options are A, D and F.