Question

Consider a spring mass system (mass m1, spring constant k) with period T1. Now consider a spring mass system with the same spring but a different mass (mass m2, spring constant k) but the period is twice as long. Compare m2 to m1 (calculate the ratio m2/m1)

Answer 1

Assuming that both mass here move horizontally on a frictionless surface, and that this spring follows Hooke's Law, then the mass of
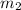`m_2` would be four times that of
`m_1`.

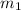Step-by-step explanation:

In general, if the mass in a spring-mass system moves horizontally on a frictionless surface, and that the spring follows Hooke's Law, then

`\displaystyle (m_2)/(m_1) = \left((T_2)/(T_1)\right)^2`.

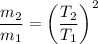Here's how this statement can be concluded from the equations for a simple harmonic motion (SHM.)

In an SHM, if the period is
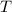`T`, then the angular velocity of the SHM would be

`\displaystyle \omega = (2\pi)/(T)`.

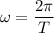Assume that the mass starts with a zero displacement and a positive velocity. If
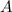`A` represent the amplitude of the SHM, then the displacement of the mass at time
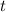`t` would be:

`\mathbf{x}(t) = A\sin(\omega\cdot t)`.

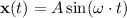The velocity of the mass at time
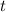`t` would be:

`\mathbf{v}(t) = A\,\omega \, \cos(\omega\, t)`.

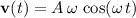The acceleration of the mass at time
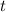`t` would be:

`\mathbf{a}(t) = -A\,\omega^2\, \sin(\omega \, t)`.

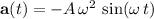Let
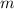`m` represent the size of the mass attached to the spring. By Newton's Second Law, the net force on the mass at time
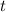`t` would be:

`\mathbf{F}(t) = m\, \mathbf{a}(t) = -m\, A\, \omega^2 \, \cos(\omega\cdot t)`,

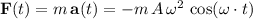Since it is assumed that the mass here moves on a horizontal frictionless surface, only the spring could supply the net force on the mass. Therefore, the force that the spring exerts on the mass will be equal to the net force on the mass. If the spring satisfies Hooke's Law, then the spring constant
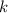`k` will be equal to:

`\begin{aligned} k &= -\frac{\mathbf{F}(t)}{\mathbf{x}(t)} \\ &= (m\, A\, \omega^2\, \cos(\omega\cdot t))/(A \cos(\omega \cdot t)) \\ &= m \, \omega^2\end{aligned}`.

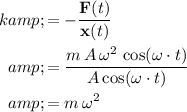Since
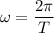`\displaystyle \omega = (2\pi)/(T)`, it can be concluded that:

`\begin{aligned} k &= m \, \omega^2 = m \left((2\pi)/(T)\right)^2\end{aligned}`.

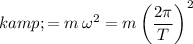For the first mass
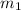`m_1`, if the time period is
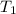`T_1`, then the spring constant would be:

`\displaystyle k = m_1\, \left((2\pi)/(T_1)\right)^2`.

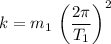Similarly, for the second mass
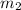`m_2`, if the time period is
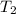`T_2`, then the spring constant would be:

`\displaystyle k = m_2\, \left((2\pi)/(T_2)\right)^2`.

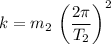Since the two springs are the same, the two spring constants should be equal to each other. That is:

`\displaystyle m_1\, \left((2\pi)/(T_1)\right)^2 = k = m_2\, \left((2\pi)/(T_2)\right)^2`.

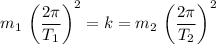Simplify to obtain:

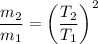`\displaystyle (m_2)/(m_1) = \left((T_2)/(T_1)\right)^2`.