Question

THIS QUESTION DOESNT MAKE ANY SENSE TO ME SO IF YOU KNOW OR COULD HELP PLEASE DO

A cone-shaped kitchen funnel has a diameter of 6 inches and a height of 7 inches. About how many times would you need to fill the funnel to fill a cylindrical can that has a radius of 4 inches and a height of 13 inches?


A. 3


B. 4


C. 9


D. 10

Answer 1

The funnel will fill the container in about 10 times

Explanation:

To solve this question, the principal thing to do is to calculate the volumes of the cone-shaped funnel and the cylinder to actually know the number of times we will need to fill the funnel so as to fill the cylinder,

These number of times can simply be calculated by dividing the volume of the cylinder by the volume of the cone-shaped funnel.

Mathematically, we proceed as follows;

Volume of the cone funnel = 1/3 ×π×
`r^(2)`× h, where r and h represents the radius and height of the cone respectively.

From the question D = 6 inches, and mathematically r = D/2 = 6/2 = 3 inches and h = 7 inches

Plugging the values we have in the question, the volume = 1/3 ×π×
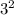`3^(2)`×7 = 21π
`inches^(3)`

For the cylindrical receptacle, we have the volume calculated as π×
`r^(2)`× h

Where r = 4 inches and h = 13 inches.

Plugging these values we have ; π ×
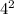`4^(2)`× 13 = 208π
`inches^(3)`

Now the number of times is simply = volume of cylindrical container/volume of cone-shaped funnel

= 208π/21π = 208/21 = 9.9 which is approximately 10 times