We have been given an equation of hyperbola
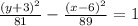 . We are asked to find the center of hyperbola.
. We are asked to find the center of hyperbola.
We know that standard equation of a vertical hyperbola is in form
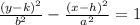 , where point (h,k) represents center of hyperbola.
, where point (h,k) represents center of hyperbola.
Upon comparing our given equation with standard vertical hyperbola, we can see that the value of h is 6.
To find the value of k, we need to rewrite our equation as:
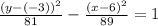
Now we can see that value of k is
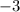 . Therefore, the vertex of given hyperbola will be at point
. Therefore, the vertex of given hyperbola will be at point
 and option D is the correct choice.
and option D is the correct choice.