Answer:
The length of AB is 16 units.
Explanation:
(a)
We know that
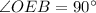 , by given, so it's a right angle, by definition.
, by given, so it's a right angle, by definition.
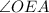 and
and
 are adjacent angles on a straight angles. That means they are sumplementary angles by definition.
are adjacent angles on a straight angles. That means they are sumplementary angles by definition.

Therefore,
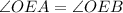 .
.
(b)
Sides AE and BE are congruent, because the congruence between those right angles, and the congruence between the other corresponding sides justify the congruence between sides AE and BE.
Notice that the hypothenuses of each right triangle are congruent, because they are also radius of the circle, which means they are congruent by definition.
Additionally, side OE is a common leg for both right triangles.
Therefore, sides AE and BE are congruent.
(c)
We know that
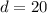 and
and
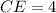 , that means the radius is
, that means the radius is
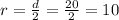
Notice that the chord AB is formed by AE and BE by sum of segments.
We know the hypothenuses are equal to 10 units of length, because they are radius.
Additionally,
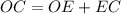 , by sum of segments.
, by sum of segments.
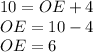
Which means the common leg is 6 units long.
Now, we use the Pythagorean's theorem to find the missing leg
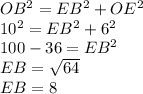
But,
 , by sum of segments.
, by sum of segments.
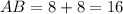 , because
, because
 we said before.
we said before.
Therefore, the length of AB is 16 units.