Answer:
0.8167
Explanation:
The exponential decay model is given as:
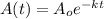 where A(t) is the present amount,
where A(t) is the present amount,
 is the initial amount, t is time in weeks and k is the decay factor.
is the initial amount, t is time in weeks and k is the decay factor.
From our problem:
A(t)=15.89kg
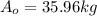
t=1 week
Therefore:

Divide both sides by 35.96

Take the natural logarithm of both sides

-k=-0.8167
k=0.8167
The decay factor from week to week is 0.8167.