Question

Name 2 characteristics of the Polar Coordinate System

Answer 1

The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. Here are two key characteristics of the polar coordinate system:

1. Radial Distance (Radius): In the polar coordinate system, the location of a point is determined first by its distance from a fixed point, called the pole, analogous to the origin in the Cartesian coordinate system. This distance is often denoted as \( r \), and it can be thought of as the radius of a circle centered at the pole, with the point lying on the circumference of this circle.

2. Angular Coordinate (Angle): The second characteristic of a point's location in the polar coordinate system is the angle
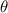`\( \theta \)` (theta), which is measured from a fixed direction, typically the positive x-axis of the corresponding Cartesian coordinate system. This angle, usually measured in degrees or radians, determines the direction of the line from the pole to the point.

These two values,
`\( r \)` and
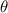`\( \theta \)`, are called polar coordinates, and they provide an alternative to the Cartesian (rectangular) coordinate system for representing points on a plane, particularly useful in scenarios where the geometry or the nature of the problem is radially symmetric, such as in the cases of circular motion or fields (gravitational, electric, etc.).

Answer 2

.I will list some characteristics:

The polar coordinates only uses 2 variables:

r, that is the radius and can have values equal or greater than zero, this is:

0 ≤ r

and θ, which is the angle, we measure the angle from the x-axis and it grows counterclockwise. An interesting this about this variable is that, while we can have any value for θ, we have that θ is a periodic variable with a period of 2*pi

So if we have θ = A, is the same that having θ = A + n*2*pi, where n can be any integer number

And we can transform the rectangular cordinates to polar cordinates by:

x = r*cos(θ)

y = r*cos(θ)