Question

6) At constant temperature, the pressure of a gas is 780 mmHg and

volume of the gas is 2.0 L. Calculate the volume of the gas when
pressure decreases to 620 mmHg.

Answer 1

2.52 L

Step-by-step explanation:

Step 1:

The following data were obtained from the question:

Initial pressure (P1) = 780 mmHg

Initial volume (V1) = 2.0 L.

Final pressure (P2) = 620 mmHg.

Final volume (V2) =?

Step 2:

Determination of the final volume of the gas.

From the question given, we discovered that the temperature is constant. Since the temperature is constant, the gas is simply obeying Boyle's law.

Applying the Boyle's law equation, the final volume of the gas can be obtained as follow:

P1V1 = P2V2

780 x 2 = 620 x V2

Divide both side by 620

V2 = (780 x 2) /620

V2 = 2.52 L

Therefore, the volume of the gas when the pressure decreases to 620 mmHg is 2.52 L

Answer 2

The volume of the gas when pressure decreases to 620 mmHg is 2.52 L

Step-by-step explanation:

Boyle's law is a law related to gases that establish a relationship between the pressure and the volume of a given amount of gas, without variations in temperature, that is, at constant temperature. So, this law establishes that at constant temperature, the volume of a fixed mass of gas is inversely proportional to the pressure it exerts.

Boyle's law is expressed mathematically as:

Pressure * Volume = constant

o P * V = k

Having a certain volume of gas V1 that is at a pressure P1 at the beginning of the experiment, if you vary the volume of gas to a new value V2, then the pressure will change to P2, and it will be true:

P1 * V1 = P2 * V2

In this case:

• P1: 780 mmHg
• V1: 2 L
• P2: 620 mmHg
• V2: ?

Replacing:

780 mmHg* 2 L= 620 mmHg* V2

Solving:

`V2=(780 mmHg* 2L)/(620 mmHg)`

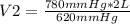
V2= 2.52 L

The volume of the gas when pressure decreases to 620 mmHg is 2.52 L