Question

Why is cos (pi/2-theta)=sin theta

Answer 1

Explanation:

Hi there,

Please recall the trigonometric identities:

`sin\theta=(O)/(H)`

`cos\theta=(A)/(H)`

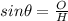
In a right triangle, there are three possible angles, one of them being 90 degrees, or π/2 radians. One of them we will designate as θ and the other φ. Since sinθ is the side opposite of it divided by hypotenuse, the cosφ is actually the same ratio! This is because although cosφ is from the other angle's perspective, what it calls "adjacent" is the opposite from perspective of θ. The same will apply if we are talking about sinφ and cosθ Draw a triangle and you will notice this using perspectives.

Since we know for a fact that it must add to π radians inside a triangle, and we already know one of them is always π/2 radians (definition of right triangle), we can do the following:

`\pi =(\pi)/(2) + \theta + \phi\\(\pi)/(2)= \theta + \phi`

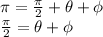
With this in mind, we have an identity for both θ and φ in terms of the other:

`\theta = (\pi )/(2) - \phi`
`\phi = (\pi )/(2) - \theta`

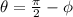
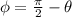
Now, based on the previous logic:

`sin\theta = cos\phi = sin((\pi)/(2) -\phi)=cos((\pi)/(2)-\theta)`

Two interesting formulas arise:

`sin\theta=cos((\pi )/(2)-\theta) \\ cos\phi= sin((\pi)/(2) -\phi)`

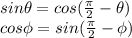
Study well and persevere.

If you liked this situation, hit a Thanks or give a Rating!

thanks,