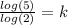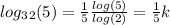Answer:
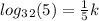
Explanation:
Let's start by using change of base property:

So, for
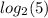
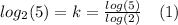
Now, using change of base for
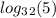
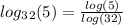
You can express
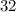 as:
as:
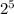
Using reduction of power property:
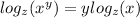
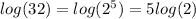
Therefore:
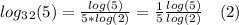
As you can see the only difference between (1) and (2) is the coefficient
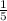 :
:
So: