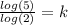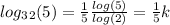Question

If log2 5 = k, determine an expression for log32 5 in terms of k.

Answer 1

`log_3_2(5)=(1)/(5) k`

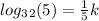
Explanation:

Let's start by using change of base property:

`log_b(x)=(log_a(x))/(log_a(b))`

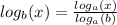
So, for
`log_2(5)`

`log_2(5)=k=(log(5))/(log(2))\hspace{10}(1)`

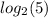
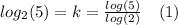
Now, using change of base for
`log_3_2(5)`

`log_3_2(5)=(log(5))/(log(32))`

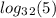
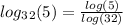
You can express
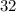`32` as:

`2^5`

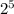
Using reduction of power property:

`log_z(x^y)=ylog_z(x)`

`log(32)=log(2^5)=5log(2)`

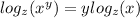
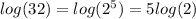
Therefore:

`log_3_2(5)=(log(5))/(5*log(2))=(1)/(5) (log(5))/(log(2))\hspace{10}(2)`

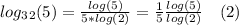
As you can see the only difference between (1) and (2) is the coefficient
`(1)/(5)` :

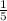So:

`(log(5))/(log(2)) =k\\`

`log_3_2(5)=(1)/(5) (log(5))/(log(2)) =(1)/(5) k`