Answer:
46.4 units^2
Explanation:
Solution:-
- We will determine the surface area of revolution of figure given below about y-axis.
- We will compute using the calculus methods and verify by using basic area formula.
- The region of solid is bound by function f ( x ) and coordinate axes.
- The function can be expressed as a linear equation of line:
y = m*x + c
Where,
m: Slope
c : y-intercept
- The slope m is evaluated by using two pair of points. We will use the end points ( 2 , 0 ) and ( 0 , 5 ) :
m = [ y2 - y1 ] / [ x2 - x1 ]
m = [ 5 - 0 ] / [ 0 - 2 ]
m = - 5 / 2 = -2.5
- The intercept is defined by coordinate ( 0 , 5 ). Where y = c = 5
- The linear function is:
y = -2.5x + 5
- From calculus the surface area of revolution of " S " about y-axis is given of the form:
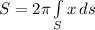
Where, ds is the differential element of solid boundary defined by the bounding function f ( x ). The formulation of integral in x-coordinate system of ds is given as:
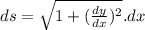
- Taking the first derivative of our bounding function y = f ( x ):
dy / dx = -2.5
- Substitute the "ds" length into the surface integral "S":
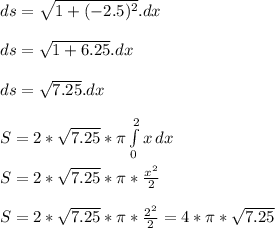
- The base area of the solid would be a circle of radius r = 2 units. The area of the circle Ac would be:
Ac = πr^2
Ac = π2^2 = 4π
-Hence,
The total surface area of the revolved region about y-axis would be:
Total Area = S + Ac
Total Area = 4π + 4π*√7.25
Total Area = 46.40236 units^2
Answer: The total area to the nearest tenth would be 46.4 unit^2.