Answer:
b. 2.01 < σ < 2.81
Explanation:
The 90% confidence interval for the population standard deviation is calculated as:
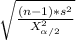 < σ <
< σ <
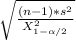
Where n is equal to 51, s is equal to 2.34,
 is 10%,
is 10%,
 is the value for the Chi squared distribution with n-1 degrees of freedom that has a probability of
is the value for the Chi squared distribution with n-1 degrees of freedom that has a probability of
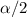 in the right tail and
in the right tail and
 is the value for the Chi squared distribution with n-1 degrees of freedom that has a probability of
is the value for the Chi squared distribution with n-1 degrees of freedom that has a probability of
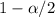 in the right tail.
in the right tail.
So, replacing n by 51, s by 2.34,
 by 67.50 and
by 67.50 and
 by 34.76, we get that the The 90% confidence interval is equal to:
by 34.76, we get that the The 90% confidence interval is equal to:
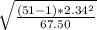 < σ <
< σ <

2.01 < σ < 2.81