Question

What is the measure of EAB in circle F?
72°
92°
148°
200°

Answer 1

148

Explanation:

Answer 2

We have been given a diagram. We are asked find the measure of arc EAB.

First of all, we will find the measure of arcs ED and CB using our given information.

We know that measure of an inscribed angle is half the measure of intercepted arc.

We can see that angle EBC is inscribed angle of arc EDC, so measure of arc EDC will be twice the measure of angle EBC.

`\widehat{EDC}=2* m\angle EBC`

`\widehat{EDC}=2* 80^(\circ)`

`\widehat{EDC}=160^(\circ)`

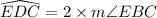
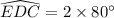
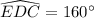
Similarly, we will find the measure of arc DCB.

`\widehat{DCB}=2* m\angle DEB`

`\widehat{DCB}=2* 70^(\circ)`

`\widehat{DCB}=140^(\circ)`

`\widehat{ED}=\widehat{EDC}-\wdiehat{DC}`

`\widehat{ED}=160^(\circ)-88^(\circ)`

`\widehat{ED}=72^(\circ)`

`\widehat{ED}+\widehat{DCB}+\widehat{EAB}=360^(\circ)`

`72^(\circ)+140^(\circ)+\widehat{EAB}=360^(\circ)`

`212^(\circ)+\widehat{EAB}=360^(\circ)`

`\widehat{EAB}=360^(\circ)-212^(\circ)`

`\widehat{EAB}=148^(\circ)`

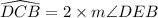
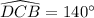
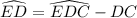
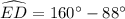
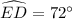
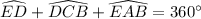
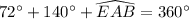
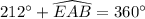
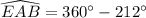
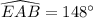
Therefore, the measure of arc EAB is 148 degrees and option C is the correct choice.