Question

A 90% confidence interval for the mean height of students

is (60.128, 69.397). What is the value of the margin of error?
a) m = 129.525
b) m = 4.635
c) m = 64.763
d) m = 9.269

Answer 1

`ME= (69.397-60.128)/(2)= 4.6345 \approx 4.635`

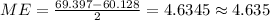
And the best answer on this case would be:

b) m = 4.635

Explanation:

Let X the random variable of interest and we know that the confidence interval for the population mean
`\mu` is given by this formula:

`\bar X \pm t_(\alpha/2) (s)/(√(n))`

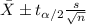
The confidence level on this case is 0.9 and the significance
`\alpha=1-0.9=0.1`

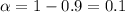
The confidence interval calculated on this case is
`60.128 \leq \mu \leq 69.397`

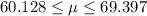
The margin of error for this confidence interval is given by:

`ME =t_(\alpha/2) (s)/(√(n))`

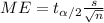
Since the confidence interval is symmetrical we can estimate the margin of error with the following formula:

`ME = (Upper -Lower)/(2)`

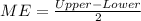
Where Upper and Lower represent the bounds for the confidence interval calculated and replacing we got:

`ME= (69.397-60.128)/(2)= 4.6345 \approx 4.635`

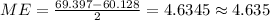
And the best answer on this case would be:

b) m = 4.635