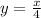Answer:
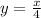
Explanation:
we find the slope which also represented as m by the formula
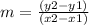
where from point (-4, -2) the x1 is -4 and the y1 is -2 and also from point (6, 3) the x2 is 6 and the y2 is 3.
so we substitute

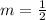
after we have the slope, we calculate the equation of the line by using the formula
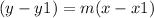
but for now, we only have y1, m and x1 so can substitute
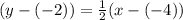
we have to get rid of the fraction 1/2 so we multiply it through by the denominator 2
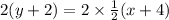
we get
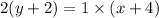
so now we expand the brackets
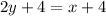
we make y stand alone by grouping liked terms.
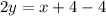
we get