Answer:
Function 1 has the least minimum value and its coordinates are (2. - 7).
Explanation:
The first function is
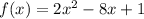
The second function is
x g(x)
-2 2
-1 -3
0 2
1 17
The vertex has coordinates of
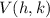 , where
, where
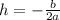 and
and
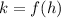 .
.
Let's find the vertex for the first function where
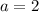 and
and
 .
.


Therefore, the vertex of the first function is at
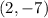 .
.
Now, the minimum value of the second function can be deducted from its table, which is
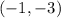 .
.
Therefore,
 has -7 as minimum value and
has -7 as minimum value and
 has -3 as minimum vale.
has -3 as minimum vale.
So, the right answer is B, because -7 is less than -3.