Question

Juan wants to know the cross-sectional area of a circular pipe. He measures the diameter which he finds, to the nearest millimeter, to be 5 centimeters.

To find the area of the circle, Juan uses the formula where A is the area of the circle and r is its radius. He uses 3.14 for π. What value does Juan get for the area of the circle? Make sure you include your units.

Answer 1

Explanation:

Hi there,

To get started, recall the area of a bound circle formula:

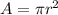`A = \pi r^(2)` where r is radius of the circle. However, Juan used an approximate value of π, 3.14. So for our purposes, the formula becomes:

`A=`
`(3.14)r^(2)`

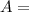
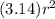
Juan measured the circle's diameter, so we can find radius from diameter first. Radius is simply twice the length of the diameter; from one circle endpoint to the center, to the endpoint across, making a straight line:

`d=2r` ⇒
`r=(d)/(2) = (5 \ cm)/(2) = 2.5 \ cm`

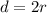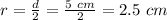
Now plug in to obtain area:

`A = (3.14)(2.5 cm)^(2) =19.625 \ cm^(2)`

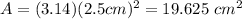
The area is 19.265 centimetres squared.

Cross-sections are the area shapes when you cut through a 3D volume; if you cut through a pipe perpendicular to where it flows, you can see it is a circle! If you cut straight through a cube, it would be a square, etc.

If you liked this solution, hit Thanks or give a Rating!

thanks,