Question

The common ratio in a geometric series is 4 and the first term is 3.

Find the sum of the first 8 terms in the series.
Show Calculator

Answer 1

The sum of the first 8 terms in the series is 65535.

Explanation:

We have,

The common ratio in a geometric series, r = 4

First term of GP is, a = 3

It is required to find the sum of the first 8 terms in the series. The sum of first n terms of a GP is given by :

`S_n=(a(r^n-1))/(r-1), r>1`

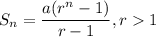
Here, n = 8

`S_8=(3* ((4)^8-1))/(4-1)\\\\S_8=65535`

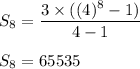
So, the sum of the first 8 terms in the series is 65535.