Question

An object is launched directly upward with an initial velocity of 64 feet per second from a platform 80 feet high. What will be the object's maximum height? When will it attain that height? When will the object reach ground level?

Answer 1

The object's maximum height is 64 feet, attained after 2 seconds. The object will reach the ground level in 4 seconds.

Step-by-step explanation:

To find the maximum height reached by the object, we can use the kinematic equation for vertical motion: h = v_0^2 / (2g), where h is the maximum height, v_0 is the initial velocity, and g is the acceleration due to gravity.

Substituting the given values into the equation, we have: h = 64^2 / (2 * 32). Solving the equation, we find that the maximum height is 64 feet.

The time it takes for the object to reach its maximum height can be found using another kinematic equation: t = v_0 / g. Substituting the given values into the equation, we have: t = 64 / 32. Solving the equation, we find that the object will attain its maximum height in 2 seconds.

The time it takes for the object to reach ground level can be found by doubling the time it took to reach the maximum height. Therefore, the object will reach the ground level in 4 seconds.

Answer 2

a) 63.6 ft

b) 1.99 seconds

c) 4.98 seconds

Step-by-step explanation:

a) The object will reach maximum height when its final velocity, v, is 0 m/s.

We apply one of Newton's equations of motion to solve this:

`v^2 = u^2 - 2gh`

where u = initial velocity = 64 ft/s

g = acceleration due to gravity = 32.2 ft/s

h = height reached by object.

Note: the equation has a negative sign because the object is going upwards, against gravity.

Hence:

`0^2 = 64^2 - 2*32.2*h\\\\=> 64.4h = 4096\\\\h = 4096 / 64.4\\\\h = 63.6 ft`

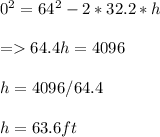
The object is now 63.6 ft above the platform (143.6 ft above the ground).

b) Time taken to get to that height can be gotten by using another one of Newton's equations:

`v = u - gt`

=>
`0 = 64 - 32.2t`

`32.2t = 64\\\\=> t = 64 / 32.2 \\\\t = 1.99 secs`

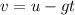
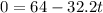
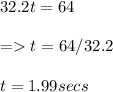
It took the object 1.99 secs to get to that height.

c) When the object begins falling to ground level, it is at a height, h = 143.6 ft and begins moving at initial velocity, u = 0 m/s.

Applying another of Newton's equations of motion, we have that:

`h = ut + (1)/(2)gt^2`

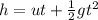
where t is the time taken to hit the floor after it begins its descent.

Therefore,

`143.6 = 0*t + (1)/(2)*32.2t^2\\ \\143.6 = 16.1t^2\\\\t^2 = 143.6 / 16.1\\\\t^2 = 8.92\\\\t = √(8.92) \\\\t = 2.99 secs`

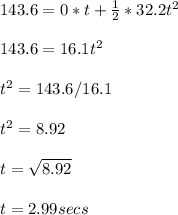
This is the time it will take the object to hit the floor after it begins its descent.

Therefore, the total time it will take for the object to hit the ground after it is launched will be:

T = time taken to reach maximum height + time taken to hit the floor after it begins descending

T = 1.99 + 2.99

T = 4.98 seconds