Question

Alice and Briana each participate in a 5 kilometer race. Alice's distance covered, in kilometers, after t minutes can be modeled by the equation a(t) =

Answer 1

a) Alice starts first, b) Briana gets the finish line first, c)
`t \approx 0.509\,min`

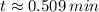
Explanation:

a) Alice starts first, since binomial inside the squared root is equal to zero when
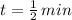`t = (1)/(2)\,min`, whereas Alice begins at
`t = 0\,min`.

b) The instant when each competitor reach finish line is:

Alice

`5\,km = (t)/(4)`

`t = 20\,min`

Briana

`5\,km = √(2\cdot t - 1)`

`25\,km^(2) = 2\cdot t - 1`

`t = 13\,min`

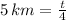
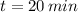
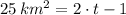
Briana gets the finish line first.

c) Alice and Briana are side by side when
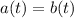`a(t) = b(t)`. Then:

`(t)/(4) = √(2\cdot t - 1)`

`(t^(2))/(16) = 2\cdot t - 1`

`t^(2) - 32\cdot t + 16 = 0`

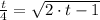
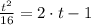
The roots of the second order polynomial are:

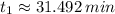`t_(1) \approx 31.492\,min` and
`t_(2) \approx 0.509\,min`

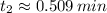
Just the second roots makes sense, as they must be side by side at one instant before getting the finish line.

Answer 2

a. Alice

b. Briana

c. 0.51 minutes

Explanation:

a. Alice formula is valid for any t > 0 minutes, but Briana formula is only valid for

2t - 1 > 0

2t > 1

t > 1/2 minutes

b. They finish when their covered distance is equal to 5 kilometers. For Alice:

t/4 = 5

t = 5*4 = 20 minutes

For Briana:

√(2t - 1) = 5

2t - 1 = 5²

2t = 25 + 1

t = 26/2

t = 13 minutes

c. They are side by side when they have covered the same distance, that is:

t/4 = √(2t - 1)

(t/4)² = 2t - 1

t²/16 = 2t - 1

t² = 16*(2t - 1)

t² = 32t - 16

t² - 32t + 16 = 0

Using quadratic formula:

`t = (-b \pm √(b^2 - 4(a)(c)))/(2(a))`

`t = (32 \pm √(-32^2 - 4(1)(16)))/(2(1))`

`t = (32 \pm 30.98)/(2)`

`t_1 = (32 + 30.98)/(2)`

`t_1 = 31.49`

`t_2 = (32 - 30.98)/(2)`

`t_2 = 0.51`

Only the second answer has sense for this problem because the race already finished before they spent 31.49 minutes in it.