Question

Belinda may choose one of two options for the method in which she may be awarded a money prize. OPTION A: Spin a spinner twice. The spinner is divided into four equally-sized sectors numbered 1, 3, 4, and 5. If the sum of the two spins is greater than 6, Belinda is awarded $8. Otherwise, she must pay $2. OPTION B: Flip a coin three times. If heads appears twice, Belinda is awarded $10. Otherwise, she must pay $2. Belinda chooses the option with the greater mathematical expectation. How much more money can Belinda expect to make by choosing this option over the other option?

Answer 1

the answer is 50 cents

Explanation:

i took the quiz lol

Answer 2

Belinda can expect to make $1 more with option B.

Explanation:

The expected value for every option is calculated as:

`E(x)=x_1*p(x_1)+x_2*p(x_2)`

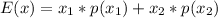
Where
`x_1` and
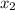`x_2` are the posibles money prize and
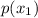`p(x_1)` and
`p(x_2)` are their respective probabilities.

Option A:

Belinda has 12 possibilities: 1-3, 1-4, 1-5, 3-1, 3-4, 3-5, 4-1, 4-3, 4-5, 5-1, 5-3 and 5-4

From that 12 possibilities, there are 6 that have a sum greater than 6. That possibilities are: 3-4, 3-5, 4-3, 4-5, 5-3 and 5-4

So, the probability that the sum of the two spins is greater than 6 is:

`P=(6)/(12) = 0.5`

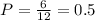
At the same way the probability that the sum of the two spins is lower or equal than 6 is 0.5.

So, the expected value for this option is:

`E_A(x)=(8*0.5)+((-2)*0.5)=3`

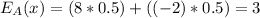
Option B:

Belinda has 8 possibilities: HHH, HHT, HTH, HTT, THH, THT, TTH and TTT

Where T means Tails and H means Heads.

Form that 8 possibilities, there are 4 which heads appear twice. That possibilities are: HHH, HHT, HTH and THH.

So, the probability that head appear twice is:

`P=(4)/(8)=0.5`

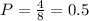
At the same way, the probability that head doesn't appear or appear once is equal to 0.5

So, the expected value for this option is:

`E_B(x)=(10*0.5)+((-2)*0.5)=4`

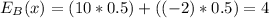
Finally, Belinda can expect to make $1 more with option B.

`E_A(x)-E_B(x)=4-3=1`