Question

There are 4 green crayons, 6 yellow crayons and 3 blue crayons. P(green

then blue) without replacement. *

Answer 1

0.0769 or 7.69%

Explanation:

Number of green crayons = 4

Number of yellow crayons = 6

Number of blue crayons = 3

Total number of crayons = 4 + 6 + 3

= 13 crayons

`Probability=\frac{\text{favorable outcome}}{\text{total number of outcome}}`

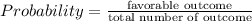
probability to get first green crayon P₁ =
`(4)/(13)`

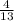
Probability to get second crayon is blue P₂ =
`(3)/(12)`

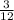
P = P₁ × P₂

=
`(4)/(13)* (3)/(12)`

=
`(12)/(156)`

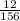
= 0.0769

Probability to get green then blue is 0.0769 or 7.69%