Answer:
The value of c is -8
Explanation:
Given
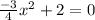
Required
The value of c, when written in a general form.
The general form of a quadratic equation is written as ax² + bx + c = 0
To get the general form of
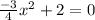 , we start by converting the fraction to whole number.
, we start by converting the fraction to whole number.
This is done by multiplying both sides of the equation by the denominator of the fraction (4)
Multiply through by 4; This gives us
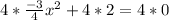

From the general form of a quadratic equation, ax² + bx + c = 0 , it'll be observed that a is positive and by comparison a = -3 (in
 )
)
So, we have to convert -3 to a positive integer by multiplying both sides of the equation by -1. This gives
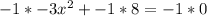
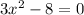
Writing
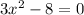 in a more general form, we have
in a more general form, we have

By comparing ax² + bx + c = 0 to

a = 3
b = 0
c = -8
Hence, the value of c is -8