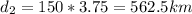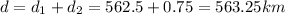Answer:
563.25 km
Explanation:
let
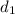 be the the distance it takes for the car to get to top speed and
be the the distance it takes for the car to get to top speed and
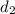 be distance traveled can be found by multiplying its top speed (150 km/h) by the number of hours that it takes for the car to finish the race. The total distance d is given as:
be distance traveled can be found by multiplying its top speed (150 km/h) by the number of hours that it takes for the car to finish the race. The total distance d is given as:
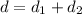
To get
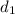 , the car is initially at rest (i.e 0 km/h) and then it accelerates to a speed of 150 km/hr within 0.01 hrs. Let u = initial velocity = 0 km/hr, v = final velocity = 150 km/hr and the time taken (
, the car is initially at rest (i.e 0 km/h) and then it accelerates to a speed of 150 km/hr within 0.01 hrs. Let u = initial velocity = 0 km/hr, v = final velocity = 150 km/hr and the time taken (
 ) = 0.01 hrs. Therefore:
) = 0.01 hrs. Therefore:
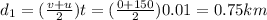
To get
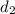 , we use the formula
, we use the formula
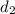 = v
= v
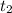 , where v =150 km / hr and
, where v =150 km / hr and
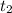 = 3.75 hrs. Therefore:
= 3.75 hrs. Therefore: