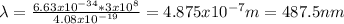Question

Hydrogen atoms absorb energy so that the electrons are excited to n=4. Calculate the wavelength, in

nm, of the photon emitted when the electron relaxes to n=2.
487nm
O 456nm
4.56 x 10 nm
4.87 x 107nm

Answer 1

the wavelength, in nm, of the photon is 487.5 nm

Step-by-step explanation:

Given:

n = 4 (excited)

n = 2 (relaxes)

Question: Calculate the wavelength, in nm, λ = ?

First, it is important to calculate the energy of the electron when it excited and then when it relaxes.

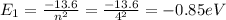`E_(1) =(-13.6)/(n^(2) ) =(-13.6)/(4^(2) ) =-0.85eV` (excited)

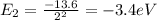`E_(2) =(-13.6)/(2^(2) ) =-3.4eV` (relaxes)

The change of energy

ΔE = E₁ - E₂=-0.85 - (-3.4) = 2.55 eV = 4.08x10⁻¹⁹J

For a photon, the wavelength emitted

`\lambda =(hc)/(delta(E))`

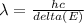
Here

h = Planck's constant = 6.63x10⁻³⁴J s

c = speed of light = 3x10⁸m/s

Substituting values:

`\lambda =(6.63x10^(-34)*3x10^(8) )/(4.08x10^(-19) ) =4.875x10^(-7) m=487.5nm`