Question

Find the value of each variable ​

Answer 1

x = 12
`√(2)`

y = 12

z = 12
`√(3)`

Explanation:

The triangle with z as one of it's sides is a 30, 60, 90 triangle where the longest side of the triangle is 2x, the shortest side as x, and the middle side as x*sqrt of 3.

The shared line between the two triangle is 12 and z is 12*sqrt of 3

The left triangle is a 45, 45, 90 triangle where the 2 sides that look the same are the same and the hypotenuse is x sqrt of 2 so y is 12 and x is 12 sqrt of 2

Answer 2

x =
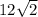`12√(2)` units

y = 12 units

z =
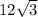`12√(3)` units

Explanation:

Notice that the biggest triangle is broken up into a 45-45-90 isosceles triangle with hypotenuse x and leg y, as well as a 30-60-90 triangle with hypotenuse 24 and long leg z.

Let's focus on finding z first. Remember that in a 30-60-90 triangle, the ratio of the short leg to the long leg to the hypotenuse is:
`1:√(3) :2`. Here, the hypotenuse is 24 and z is the longest leg, so we have the proportion:

`(√(3) )/(2) =(z)/(24)`

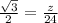
Cross-multiply:

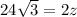
`24√(3) =2z`

z =
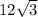`12√(3)` units

Now, let's find the smallest leg of the 30-60-90 triangle; it is simply 24/2 = 12 units. Let's move onto x and y.

Remember that in a 45-45-90 triangle, the ratio of one leg to the second leg to the hypotenuse is:
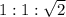`1:1:√(2)`. So, since y is a leg of this triangle and the smallest leg of the 30-60-90 triangle coincides with the second leg of the 45-45-90 triangle, y = 12 units.

Finally, x is found by multiplying 12 by
`√(2)`: 12 *
`√(2)` =
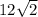`12√(2)` units

Hope this helps!