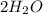Answer:
a) 13.2 moles
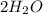
b) 79.33 grams of
Step-by-step explanation:
First, we'll need to balance the equation
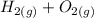 →
→

There are 2 (O) on the left and only one on the right, so we'll add a 2 coefficient to the right.
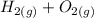 →
→
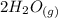
Now there are 4 (H) on the right and only 2 on the left, so we'll add a 2 coefficient to the (
 ) on the left.
) on the left.
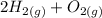 →
→
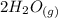
The equation is now balanced.
a) This can be solved with a simple mole ratio.
4.6 moles
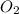 ×
×
 = 13.2 moles
= 13.2 moles
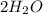
b) This problem is solved the same way!
2.2 moles
 ×
×
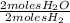 = 2.2 moles
= 2.2 moles
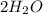
However, this problem wants the mass of
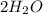 , not the moles.
, not the moles.
The molecular weight of
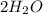 is the weight of 4 (H) molecules and 2 (O) molecules (found on the periodic table). So,
is the weight of 4 (H) molecules and 2 (O) molecules (found on the periodic table). So,
4(1.008) + 2(15.999) = 36.03 g/mol
2.2 moles
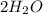 ×
×
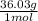 = 79.33 grams of
= 79.33 grams of