Question

In the figure below, if C is the center of the circle and 30 < C < 60, then which of the following expresses all possible values of a?

Select one:

A. 50 < a < 70

B. 60 < a < 70

C. 60 < a < 75

D. 75 < a < 90

E. 100 < a < 115

Answer 1

Option C.

Explanation:

In the given figure C is the center of the circle.

Let A and B are two points on the circle, such that

`\angle A=a^(\circ),\angle B=b^(\circ)`

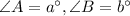
Since CA and CB are radius of the circle, therefore ABC is an isosceles triangle.

`\angle A=\angle B=a^(\circ)`

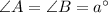
Using angle sum property,

`\angle A+\angle B+\angle C=180^(\circ)`

`a^(\circ)+a^(\circ)+\angle C=180^(\circ)`

`2a^(\circ)=180^(\circ)-\angle C`

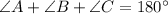
Divide both sides by 2.

`a^(\circ)=(180^(\circ)-\angle C)/(2)`

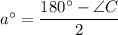
It is given that

`30<C<60`

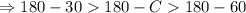`\Rightarrow 180-30>180-C>180-60` (Subtract from 180)

`\Rightarrow 150>180-C>120`

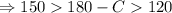
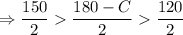`\Rightarrow (150)/(2)>(180-C)/(2)>(120)/(2)` (Divide by 2)

`\Rightarrow 75>a>60`

`\Rightarrow 60<a<75`

Hence, the correct option is C.