Question

Jackson purchases a new car for $48,000. The car's value can be modeled by the

following exponential function: y = 48000(0.76)^t where y represents the car's
value and t represents time in years. What is the decay rate expressed as a
percentage? *

Answer 1

We have been given that Jackson purchases a new car for $48,000. The car's value can be modeled by the following exponential function:
`y = 48000(0.76)^t` where y represents the car's value and t represents time in years. We are asked to find the decay rate as a percentage.

We know that an exponential decay function is in form
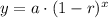`y=a\cdot (1-r)^x`, where,

y = Final value,

a = Initial value,

r = Decay rate in decimal form,

x = time.

Upon comparing our given function
`y = 48000(0.76)^t` with standard decay function
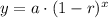`y=a\cdot (1-r)^x`, we can see that
`1-r=0.76`.

Let us solve for r.

`1-1-r=0.76-1`

`-r=-0.24`

`r=0.24`

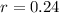
Let us convert 0.24 into percentage.

`0.24* 100\%=24\%`

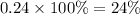
Therefore, the decay rate is 24%.