Question

Darren invests $4,500 into an account that earns 5% annual interests. How much will be in the account after 10 years if the interest rate is compounded annually, quarterly, monthly, or daily? Which compounded interest rate should Darren choose?

Answer 1

We have been given that Darren invests $4,500 into an account that earns 5% annual interests. We are asked to find the amount in his account after 10 years, if the interest rate is compounded annually, quarterly, monthly, or daily.

We will use compound interest formula to solve our given problem.

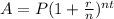`A=P(1+(r)/(n))^(nt)`, where,

A = Final amount,

P = Principal amount,

r = Annual interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

`5\%=(5)/(100)=0.05`

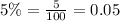
When compounded annually,
`n=1`:

`A=4500(1+(0.05)/(1))^(1\cdot 10)`

`A=4500(1.05)^(10)`

`A=4500(1.6288946267774414)`

`A=7330.025820498\approx 7330.03`

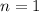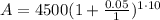
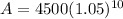
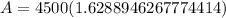
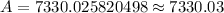
When compounded quarterly,
`n=4`:

`A=4500(1+(0.05)/(4))^(4\cdot 10)`

`A=4500(1.0125)^(40)`

`A=4500(1.6436194634870132)`

`A=7396.28758569\approx 7396.29`

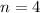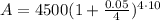
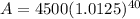
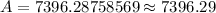
When compounded monthly,
`n=12`:

`A=4500(1+(0.05)/(12))^(12\cdot 10)`

`A=4500(1.00416666)^(120)`

`A=4500(1.64700949769)`

`A=7411.542739605\approx 7411.54`

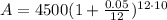
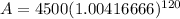
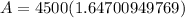
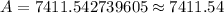
When compounded daily,
`n=365`:

`A=4500(1+(0.05)/(365))^(365\cdot 10)`

`A=4500(1.0001369863013699)^(3650)`

`A=4500(1.6486648137656943695)`

`A=7418.9916619456\approx 7419.00`

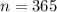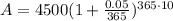
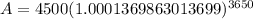
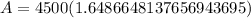
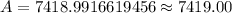
Since amount earned will be maximum, when interest is compounded daily, therefore, Darren should use compounded daily interest rate.