Question

A farmer uses 36 feet of fencing to build a rectangular rabbit pen. The function

A(W) = 18w – wê can be used to find the area of the pen for a given width, w
What is the greatest possible area the farmer can enclose in a rectangular pen
with 36 feet of fencing?

Answer 1

81 square feet

Explanation:

Given the function

A(W) = 18w –
`w^(2)`

To find the greatest possible area the farmer can enclose in a rectangular pen

with 36 feet of fencing, we take the derivative on both sides of the function:

A'(w) = 18 -2w

=> A''(w) = -2

Since A"(w) is in negative, so the critical value will yield maximum value of the function.

So, A'(w) = 0

<=> 18 -2w = 0

<=> w = 9

Substitute w= 9 into the A(W) = 18w –
`w^(2)` , we have the greatest possible area is:

= 18*9 -
`9^(2)`

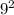
= 81 square feet