Question

Decide whether y is a function of x.
x2 + y2 = 1

Answer 1

A function can be described as one-to-one or many-to-one, i.e. each value in the domain (
`x`-values) is mapped to a single value in f(x).

An example of a one-to-one function is a linear function. For every value of x there is one value of y.

An example of a many-to-one function is a quadratic function, where 2 different x-values map to one y-value.

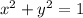`x^2+y^2=1` is not a function as some values of
`x` are mapped to two different values of f(x).

For example, let x = 0.5

`\implies (0.5)^2+y^2=1`

`\implies y^2=0.75`

`\implies y=\pm√(0.75)`

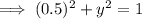
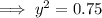
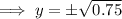
So as x = 0.5 maps to √0.75 and -√0.75, it is one-to-many, and is therefore not a function.

Answer 2

Not a function.

Step-by-step explanation:

x² + y² = 1 is not a function.

Here's the breakdown!

Looking at the type of equation, It is a circle equation.

In a circle equation, y value is not completely determined by the x value.

Shown:

• x² + y² = 1

• y² = 1 -x²

• y = ±√1 -x²

There are multiple values of x for each value of y