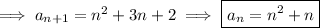Check the forward differences of the sequence.
If
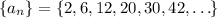 , then let
, then let
 be the sequence of first-order differences of
be the sequence of first-order differences of
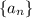 . That is, for n ≥ 1,
. That is, for n ≥ 1,
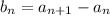
so that
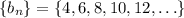 .
.
Let
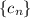 be the sequence of differences of
be the sequence of differences of
 ,
,
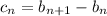
and we see that this is a constant sequence,
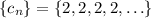 . In other words,
. In other words,
 is an arithmetic sequence with common difference between terms of 2. That is,
is an arithmetic sequence with common difference between terms of 2. That is,
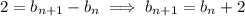
and we can solve for
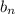 in terms of
in terms of
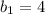 :
:
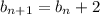
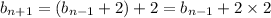

and so on down to
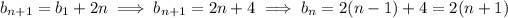
We solve for
 in the same way.
in the same way.
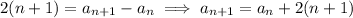
Then
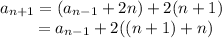
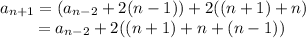

and so on down to