Question

What is the longest-wavelength EM radiation that can eject a photoelectron from silver, given that the binding energy is 4.73 eV? Is this in the visible range?

Answer 1

The longest wavelength is
`\lambda = 263\ nm`

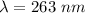
It is not in the range of visible light

Step-by-step explanation:

From the question the question we are told that

The binding energy is
`E = 4.73 \ eV`

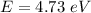
the kinetic energy of the ejected photoelectron is mathematically represented as

`KE = hf - E`

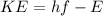
Where h is the plank constant with a values of
`h = 4.14 *10^(-15)eV \cdot s`

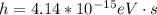
f is the frequency of the the EM which is mathematically represented as

`f = (c)/(\lambda )`

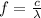
Here c is the speed of light with value
`c = 3.0 *10^(8) m/s`

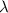`\lambda` is the wavelength

So we have

`KE = h[(c)/(\lambda) ] - E`

So making
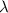`\lambda` the subject of the formula

`\lambda = (hc)/([KE +E ])`

Here the maximum kinetic energy is zero this is because out of all the electron ejected using a light of a threshold frequency (i.e a photo electron ) the one that has the maximum kinetic energy is none so this implies that maximum kinetic energy is zero so the equation becomes

`\lambda = (4.4 *10^(-15) * 3.00 *10^(8))/((0 + 4.73))`

`\lambda = 263\ nm`

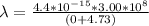
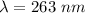
Looking at this we see that it is not in the range of visible light which is

400nm - 700nm