Answer:
a)

b) 0.6957
Explanation:
Let X represent the number of 4's when n = 5 independent spins
each has a probability of 0.2 (i.e p = 0.2)
This notation is represented as:
X
 Binomial (n = 5, p = 0.2)
Binomial (n = 5, p = 0.2)
Probability of
 number of 4's is:
number of 4's is:
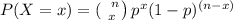
here;
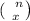 is the combinatorial expression
is the combinatorial expression
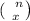 =
=
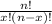
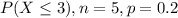
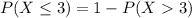
So; let's first find:
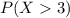

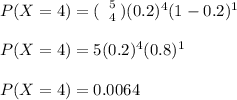

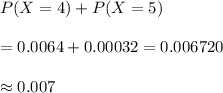
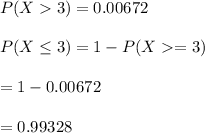

b)
Given that:
The ratio of boys to girls at birth in Singapore is quite high at 1.09:1
What proportion of Singapore families with exactly 6 children will have at least 3 boys?
Probability of having a boy =
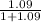 = 0.5215
= 0.5215
Binomial Problem with n = 6
P(3<= x <=6) = 1 - P(0<= x <=2)
= 1 - binomial (6,0.5215,2)
= 0.6957