Question

Kesha threw her baton up in the air from the marching band platform during practice. The equation h(t) = −16t² + 54t + 40 gives the height of the baton, in feet, t seconds after it is thrown from the platform. What is the height of the platform? At what speed was the baton thrown? If she doesn't catch it, when will it hit the ground?

Answer 1

(a)Height of the platform=40 feet

(b)Initial Velocity=54 ft/sec

(c)4 seconds

Explanation:

The equation
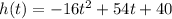`h(t) = -16t\² + 54t + 40` gives the height of the baton, in feet, t seconds after it is thrown from the platform.

(a)Height of the platform

The Height of the platform is the height at which t=0

`h(0) = -16(0)\² + 54(0) + 40`

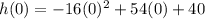
Height of the platform=40 feet

(b)To determine the speed at which the baton was thrown, we find the velocity, v(t).

`v(t)=(dh)/(dt) =(d)/(dt) (-16t\² + 54t + 40)=-32t+54\\$At t=0\\v(0)=-32(0)+54=54 feet/sec`

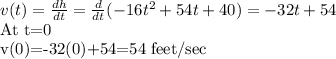
(c)The baton will hit the ground when its height, h(t)=0

`-16t\² + 54t + 40=0\\\text{Solving the quadratic formular}\\t = (-54\pm √((-54)^2 - 4*40*(-16)) )/(2*-16)\\= (-54\pm √(5476 ))/(-32)\\= (-54\pm 74)/(-32)\\t=(-54+ 74)/(-32),(-54- 74)/(-32)\\t=-0.625\:or \:t=4`

Since -0.625 is not valid, the baton will hit the ground 4 seconds after it is thrown.