Question

The grade point averages (GPA) for 12 randomly selected college students are shown on the right. Complete parts (a) through (c) below.

Assume the population is normally distributed.

2.3 3.1 2.8
1.7 0.9 4.0
2.1 1.2 3.6
0.2 2.4 3.2

Find the standard deviation

Answer 1

X ~ Norm ( 2.29167 , 1.09045^2 )

Explanation:

Solution:-

- The (GPA) for 12 randomly selected college students are given as follows:

2.3 , 3.1 , 2.8 , 1.7 , 0.9 , 4.0 , 2.1 , 1.2 , 3.6 , 0.2 , 2.4 , 3.2

- We are to assume the ( GPA ) for the college students are normally distributed.

- Denote a random variable X: The GPA secured by the college student.

- The normal distribution is categorized by two parameters:

- The mean ( u ) - the average GPA of the sample of n = 12. Also called the central tendency:

`Mean ( u ) = (\sum _(i=1)^(\ 12 )\: Xi )/(n)`

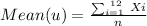
Where,

Xi : The GPA of the ith student from the sample

n: The sample size = 12

`Mean ( u ) = (2.3 + 3.1 + 2.8 + 1.7 + 0.9 + 4.0 + 2.1 + 1.2 + 3.6 + 0.2 + 2.4 + 3.2)/(12) \\\\Mean ( u ) = (27.5)/(12) \\\\Mean ( u ) = 2.29167`

- The other parameter denotes the variability of GPA secured by the students about the mean value ( u ) - called standard deviation ( s ):

`s = \sqrt{(\sum _(i=1)^(\ 12 )\: [ Xi - u]^2)/(n) } \\\\\\\sum _(i=1)^(\ 12 )\: [ Xi - u]^2 = ( 2.3 - 2.29167)^2 + ( 3.1 - 2.29167)^2 + ( 2.8 - 2.29167)^2 + ( 1.7\\\\ - 2.29167)^2+ ( 0.9 - 2.29167)^2 + ( 4 - 2.29167)^2 + ( 2.1 - 2.29167)^2 + ( 1.2 - 2.29167)^2 +\\\\ ( 3.6 - 2.29167)^2 + ( 0.2 - 2.29167)^2 + ( 2.4 - 2.29167)^2 + ( 3.2 - 2.29167)^2 \\\\\\\sum _(i=1)^(\ 12 )\: [ Xi - u]^2 = 14.26916 \\\\\\s = \sqrt{( 14.26916 )/(12) } \\\\s = √(1.18909 ) \\\\s = 1.09045`

- The normal distribution for random variable X can be written as:

X ~ Norm ( 2.29167 , 1.09045^2 )

Answer 2

`\bar X =(2.3+3.1+2.8+1.7+0.9+4+2.1+1.2+3.6+0.2+2.4+3.2)/(12)=2.29`

`s=1.09`

Explanation:

For this case we have the following data given:

2.3 3.1 2.8

1.7 0.9 4.0

2.1 1.2 3.6

0.2 2.4 3.2

Since the data are assumedn normally distributed we can find the standard deviation with the following formula:

`\sigma =\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n)}`

And we need to find the mean first with the following formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\bar X =(2.3+3.1+2.8+1.7+0.9+4+2.1+1.2+3.6+0.2+2.4+3.2)/(12)=2.29`

And then we can calculate the deviation and we got:

`s=1.09`